| Step of Proof: absval_wf |
12,41 |
|
Inference at *
Iof proof for Lemma absval wf:
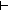
 x:
x: . |x|
. |x| 

 by ((((Unfold `absval` 0)
by ((((Unfold `absval` 0)
 CollapseTHEN (D 0))
CollapseTHEN (D 0)) )
)
 CollapseTHENA ((Auto_aux (first_nat 1:n
CollapseTHENA ((Auto_aux (first_nat 1:n
 C) ((first_nat 1:n),(first_nat 3:n)) (first_tok :t) inil_term)))
C) ((first_nat 1:n),(first_nat 3:n)) (first_tok :t) inil_term)))
 C1:
C1:
 C1: 1. x :
C1: 1. x : 
 C1:
C1: 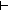 if 0
if 0  z x then x else -x fi
z x then x else -x fi 

 C.
C.